15.05/
9 клас, алгебра
- виконати за підручником № 3.3, 3.5, 3.8 (1-6) відкрити підручник
- інтерактивна вправа "Вершина параболи" відкрити вправу
- інтерактивна вправа "Графік кв.функції" відкрити вправу
9 клас, алгебра
28.04.Привіт.
Арифметична прогресія, сума арифметичної прогресії
Означення: Арифметична прогресія  — числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число.
— числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число.
 — числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число.
— числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число.
Означення: Різниця арифметичної прогресії  — постійне для послідовності число
— постійне для послідовності число 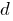 , яке додають до кожного члена.
, яке додають до кожного члена.
 — постійне для послідовності число
— постійне для послідовності число 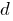 , яке додають до кожного члена.
, яке додають до кожного члена.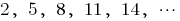 — зростаюча арифметична прогресія
— зростаюча арифметична прогресія 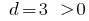
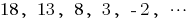 — спадна арифметична прогресія
— спадна арифметична прогресія 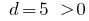
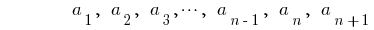 —арифметична прогресія
—арифметична прогресія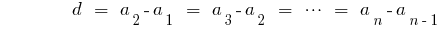 —різниця арифметичної прогресії
—різниця арифметичної прогресіїХарактеристичні властивості арифметичної прогресії
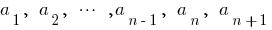
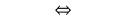
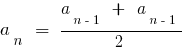
Властивість: Будь-який член арифметичної прогресії, починаючи з другого, лорівнює середньому арифметичному попередньогоі настпного члена і навпаки, якщо виконується зазначена влстивість, то послідовність буде арифметичною прогресією.
Формули n-ого члена арифметичної прогресії
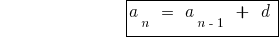
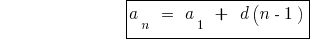
Формули суми n перших членів арифметичної прогресії
Сума перших п членів арифметичної прогресії
|
1. Якщо a1 і an — перший і п-й члени арифметичної прогресії (аn), то сума Sn перших п членів цієї прогресії дорівнює:
|
2. Якщо a1 і d — перший член і різниця арифметичної прогресії (ап), то сума Sn перших п її членів дорівнює:
|
Приклад. Знайдемо суму перших десяти членів арифметичної прогресії (аn), у якої:
1) a1 = 10, а2 = -10; 2) а1 = 2, d = -3.
Розв'язання
|
1) S10 =
|
2) S10 =
= -23 ∙ 5 = -115.
Відповідь: 1) 0; 2) -115.
|
Усні вправи
1. Задана скінченна послідовність: (аn): 2; -1; 5; -2; 9; -3; 15; -4. Знайдіть суму:
1) перших двох її членів;
2) перших п'яти її членів;
3) усіх її членів.
1. Знайдіть суму перших тридцяти членів арифметичної прогресії (хп), у якої х1 = 5, х30 = 15.
2. Знайдіть суму перших десяти членів арифметичної прогресії (уп), у якої y1 = 5, d = 3, заповнивши пропуски у формулі  .
.
Письмові вправи
1) за однією з вивчених формул знайти (обчислити) суму перших п членів арифметичної прогресії;
2) розв'язати задачі, що передбачають пряме застосування вивчених формул (в умові задач напряму не сказано, що шукана сума є сумою арифметичної прогресії), наприклад, знайти суму перших 50 натуральних чисел або знайти суму парних натуральних чисел від 0, не більших за 100, і т. д.;
3) задачі на застосування вивчених формул для відшукання невідомих першого члена, або різниці, або кількості пчленів арифметичної прогресії за відомою за умовою сумою її перших членів;
4) на повторення: задачі на застосування вивчених властивостей і формул арифметичної прогресії.
Контрольні запитання
1. За якою формулою можна обчислити суму перших ста членів арифметичної прогресії, якщо відомі:
1) а1 і а100; 2) а1 і d; 3) а1 і а2?
2. Чи можна за формулою  обчислити суму перших десяти членів послідовності:
обчислити суму перших десяти членів послідовності:
1) (аn): 2; 3; 4; 5; 6; ...;
2) (аn): 2; 4; 8; 16; 32; ...;
3) (ап): n; 3n; 5n; 7n; 9n;
Домашнє завдання
1. Вивчити формули (див. опорний конспект ).
2. Розв'язати вправи, аналогічні за змістом та рівнем складності виконаним на уроці;
3. Повторити: означення числової послідовності, формули, вивчені в темі «Арифметична прогресія» та властивості
Опрацювати конспект та виконати завдання в зошиті
Знайдіть суму:
1) перших шістнадцяти членів арифметичної прогресії, якщо її перший і шістнадцятий члени відповідно дорівнюють 3 і -5;
2) перших шістнадцяти членів арифметичної прогресії, якщо її перший член дорівнює 6, а різниця 3;
3) перших сорока семи членів арифметичної прогресії, яка задана формулою загального члена ап = 3п – 1;
Немає коментарів:
Дописати коментар